Learning notes_2018_11
🐯 有关病毒标记
🍧 顺行标记:沿信号传递方向,一般的病毒,常用AAVs
🥧 逆行标记:沿信号传递相反的分向,狂犬病毒,常用Rv
🍻 跨突触标记:多神经元传递
🍥 条件概率、贝叶斯公式和全概率公式
🍼 边缘概率(又称先验概率):某个事件发生的概率。
边缘概率 是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
🥜 联合概率表示两个事件共同发生的概率。A与B的联合概率表示为P ( A \bigcap B )或者P(A,B)。
🍣 条件概率(又称后验概率):事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
条件概率:
贝叶斯公式:
全概率公式:
全概率公式和贝叶斯公式的结合
🏋️ 无偏估计、有效性、一致性
🚵 无偏估计
估计量数学期望等于被估计参数真实值,则称此此估计量为被估计参数的无偏估计,即具有无偏性。
无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。
🚴 有效性
估计量方差越小,则说明这个估计量有效性更高。
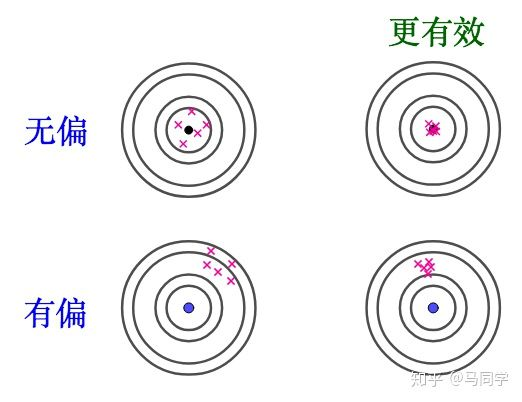
有效性和无偏估计不相关
🎯 一致性
一致性就是在大样本条件下,估计值接近真实值。
🎮 额叶皮层
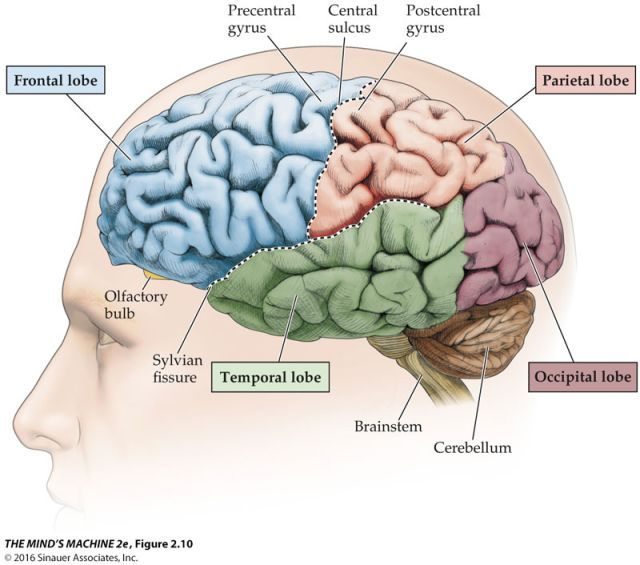
前额叶指的是额叶的前端。
要了解前额叶的位置,我们应该先了解额叶的位置。大脑的两个半球通常被分为四个脑叶,分别是:
🔩 额叶(Frontal lobe)
🎈 顶叶(Parietallobe)
📄 颞叶(Temporallobe)
📙 枕叶(Occipitallobe)
额叶和顶叶由中央沟(Central sulcus)隔开;
外侧裂(Sylvianfissure)则将颞叶与额叶、顶叶分隔开;
大脑背侧的顶枕沟(Parieto-occipital sulcus)和腹外侧的枕前切迹(Preoccipital notch)则将枕叶与顶叶、颞叶分隔开。
额叶的前端是前额叶,前额叶的表层便是前额叶皮层,主要与人类的高级认知功能相关;
额叶后端的表层是运动皮层,主要与运动的控制相关。
💖 图像的复原方法
MATLAB的图像处理工具箱中提供了四种图像复原的函数,分别利用:
维纳滤波器(wiener)复原
规则化滤波器(regularized)复原
Lucy-Richardson方法复原
盲反卷积复原
图像复原的四种函数
其中:
1. deconvwnr函数求得的是最小二乘解
2. deconvreg 函数求得的是一种约束最下二乘解,在使用此函数时若提供一些关于噪声的参数可以减少去模糊过程中噪声的放大作用。
3. deconvlucy 函数使用的是一种快速抑制的Lucy-Richardson方法, 经过多次迭代,采用优化技术和泊松统计准则,不需要函数提供模糊图像中关于噪声的额外参数。
4. 使用deconvbind函数时不需要知道真实的点扩散函PSF,使用盲反卷积技术,只需要初始设置一个PSF参数,函数除了返回恢复出的图像外,还返回最后跌倒的点扩散函数PSF。
🕑 朴素贝叶斯算法及贝叶斯估计
定义:贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称贝叶斯分类。而贝叶斯分类中最简单的一种:朴素贝叶斯分类。
朴素贝叶斯分类:基于特征条件独立假设,学习输入输出的联合概率分布,对于输入x,朴素贝叶斯法求出后验概率最大的输出y,这等价于期望风险最小化。
朴素贝叶斯法的参数估计:极大似然估计。
贝叶斯估计:用极大似然估计可能出现要估计的概率值为0的情况,这会影响到后验概率的计算结果,使分类产生偏差,解决这类问题的方法是采用贝叶斯估计。

🚩 概念定义
🏁 凸集:欧式空间中,对于集合中的任意两点的连线,连线上任意一点都在集合中,我们就说这个集合是凸集。
➗ 凸函数:对于任意属于\[0,1\]的a和任意属于凸集的两点x, y,有f( ax + (1-a)y ) <= a f(x) + (1-a) f(y),几何上的直观理解就是两点连线上某点的函数值,大于等于两点之间某点的函数值。凸函数的任一局部极小点也是全局极小点
💭 半正定矩阵:特征值大于等于0的实对称矩阵。
半正定矩阵的充要条件:行列式(n阶顺序主子式)等于0,行列式的i阶顺序主子式>=0,i从1到n-1
📣 凸函数的充要条件:如果f(x)在开凸集S上具有二阶连续偏导数,且f(x)的海塞矩阵(二阶偏导的矩阵)在S上处处半正定,则f(x)为S上的凸函数。
🖌 酉矩阵:酉矩阵的共轭转置和它的逆矩阵相等。
